Ask an Expert: What is Celestial Navigation?

A midshipman takes a sextant reading. Image credit: Wikimedia

Using the stars to navigate the way, whether on land, at sea, in the air or in space—otherwise known as ‘celestial navigation’—has been used for many years by humans. What exactly is it and how does it work? UNSW Canberra’s Dr Lily Qiao shows us how expansive the world of celestial navigation is.  

What is celestial navigation? 

Before the emergence of radio navigation, celestial navigation was the primary marine navigation method of seafaring navigators, where there were no landmarks for centuries. To date, celestial navigation has expanded its application to aircraft, missiles and space systems. For space, it can serve Low Earth Orbit, High Earth Orbit satellites, deep space probes and planetary rovers. Celestial navigation might be the only feasible method to guide spacecraft to the far reach of the solar system, where nothing but celestial bodies are around. 

Celestial navigation uses natural celestial bodies (such as the Sun, the Moon and stars) as navigation beacons to calculate the position of the observation point. The positions of celestial bodies in the inertial frame are known and can be tabulated in the published nautical or air almanac almanacs. The almanacs tell the position of the celestial bodies at different times of the year. For Southern Hemisphere countries like Australia, the most familiar constellation is the Southern Cross. In Northern Hemisphere, people are more familiar with the Polaris and the Big Dipper. Sailors use a sextant to measure the angles between the celestial bodies and the horizon. When they are moving, the observed angles will change accordingly. Then, we could calculate the position and head of the observation point with these observations.  

How does celestial navigation work? 

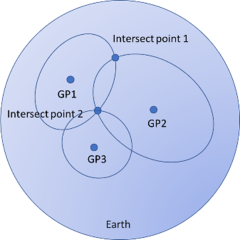
Celestial navigation is a position-fixing practice. Therefore, we use the circle drawing method to find the intersection point to determine the position of the observation point.  

The principle of celestial navigation

First, the sailors need to identify a celestial body and find the location of the geographic position (GP) of the celestial body by looking at the almanacs. GP is the point where a straight line from the celestial body to the centre of the Earth. Use this GP as a centre and then draw a circle whose radius is the shortest distance from the centre to the observation point on the sphere. The radius can be calculated using the angle between the celestial body and the horizon observed measured by sextant, also called the altitude of a celestial body. If the angle is h, the radius is 90-h degree. One degree equals one nautical mile or minute of arc. This circle is called the circle of equal altitude, and we are someplace in this circle. Then, we need to take an observation of another celestial body to determine a fixed position. Two intersections will be noticed, but only one will be near the ship's actual position on a nautical chart. If we observe a third celestial body, one point is specified where all three circles' interests are. The principle of celestial navigation for planetary rovers is the same. The difference is that Mars rovers will use the Mars-centred almanacs rather than Earth-centred ones. 

The way to sense the horizon is different for earth satellites' position determination and deep space probers. Satellites use earth sensors or starlight refraction models from star sensors to obtain the horizon information. The former is used in Microcosm Autonomous Navigation Systems (MANS), which used the sun, the moon, earth horizon and star measurements combined with a Kalman Filter to determine the orbit and attitude. The latter was used in the US space experiment called the Multitask Autonomous Navigation System (MADAN) in the 1990s. Deep space probes can also use earth and moon limbs or the images of asteroids as measurements. 

Recently, a new celestial navigation method that uses X-ray pulsars (XNAV) as navigation beacons has been explored. Pulsars are rapidly rotating neutron stars that emit pulsed electromagnetic radiation. These pulsars are natural lighthouses. We can compare the measured and predicted pulse time of arrival and then calculate the position, attitude and time for space probes in the solar system.